「場合の数」は、サイコロの目の出方のように、ある事柄が起こるとき「何通り起こるか」を数え上げる単元です。中学受験で頻出なだけでなく、高校受験や大学受験にも出題されるテーマなので、しっかりマスターしておきましょう。

◆本記事の目次

「場合の数」が苦手な理由

場合の数の問題は中学受験の算数でよく出題されるため、解き方をしっかり理解して確実に得点したい単元で、場合の数が苦手だと感じているケースでは、次のような原因が考えられます。

●数え間違いをしている

場合の数では、カードの選び方やサイコロの目の出方など、ある事柄が起きる回数を正しく数えなければなりません。場合の数の問題が解けない理由の一つは、重複して数えていたり、数え漏れをしているといった、数え間違いをしていることがあげられます。

●そもそも数え方がわからない

場合の数は、「順列」や「組み合わせ」などのルールにのっとって数える必要がありますが、まずそのルールを知らないと正しく数えられません。また、サイコロの目の出方やカード・人の並べ方、色の塗り分け、道順など、問題のパターンが多様であるため、どの問題でどの数え方を使えばよいのかを見極める点に、難しさを感じていると考えられます。

---

「場合の数」をスムーズに解くコツ

場合の数は中学受験だけではなく、高校受験や大学受験にも出題されるテーマです。小学生のうちに基本的な考え方や解法を、しっかり身につけておきましょう。

●樹形図を画く

場合の数を数えるために必須の知識、樹形図の画き方です。樹形図を画くことで問題の内容がすっきりと視覚的に整理され、過不足なく数えやすくなります。また、樹形図を用いて考えることで、順列・組み合わせの公式や和の法則・積の法則についても、ただ暗記するだけではなく、なぜそうなるのかを理解することができます。

●問題のパターンを覚える

場合の数の問題は、サイコロの目の出方やカードの並べ方など、多くのパターンがありますが、どの数え方をするパターンなのかを見極めることができれば、解くことができます。解法のパターンを見極める力をつけるためには、いろいろなパターンの問題にあたり、繰り返し解くことが有効です。

---

中学受験でよく出る「場合の数」の例題と解き方

場合の数の基本的な例題を４つあげています。どのように数えればよいか考えてみましょう。

●例題１【順列】

・問題
Ａ君、Ｂ君、Ｃ君、Ｄ君の４人でボール投げをしました。４人が投げる順番は何通りあるか求めなさい。

・答えと解き方
答え：24通り

まず、Ａ君が１番目に投げる場合の樹形図を画きます。Ａ君が１番目なので、２番目に投げるのは、Ｂ君、Ｃ君、Ｄ君のいずれかです。２番目がＢ君だとすると、３番目、４番目に投げるのは、Ｃ君、Ｄ君となる場合とＤ君、Ｃ君となる場合の２通りです。２番目がＣ君、Ｄ君の場合も、同じようにそれぞれ２通りずつあるので、１番目にＡ君が投げる場合は、２×３＝６（通り）あります。同様に、１番目にＢ君、Ｃ君、Ｄ君が投げる場合を考えればよいので、４人がボールを投げる順番は、６×４＝24(通り)です。

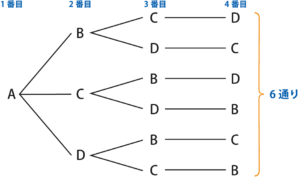
・解き方のポイント
この問題のように、「いくつかのものを順番に並べる並べ方」を数える順列の問題では、樹形図を画くのがポイントです。「４人が投げる順番」→「４人を投げる順番に並べる」と頭の中で変換できれば、順列の問題であることがわかるでしょう。
４人がボールを投げる条件は同じなので、Ａ君が１番に投げる場合の数が樹形図から求められれば、それに４を掛ければよいことがわかります。

・別の解き方
順列の問題であるとわかれば、順列の公式を使って解くこともできます。この問題では、４人全員を並べるので、４×３×２×１＝24（通り）となります。

●例題２【組み合わせ】

・問題
Ａ君、Ｂ君、Ｃ君、Ｄ君の４人の中から学級委員を２人選ぶとき、選び方は何通りあるか求めなさい。

・答えと解き方
答え：６通り

この問題も、樹形図を画いて数えてみましょう。まず、Ａ君が選ばれる場合の数を考えると、もう１人はＢ君、Ｃ君、Ｄ君の誰かなので３通りです。次に、Ａ君以外が選ばれる場合を考えます。Ｂ君が選ばれる場合の数は、もう１人がＣ君かＤ君のどちらかなので２通りです。このとき、「Ａ君とＢ君」「Ｂ君とＡ君」は同じ選び方ですから、「Ｂ君とＡ君」の選び方を数えないように注意しましょう。最後に、Ａ君、Ｂ君以外が選ばれる場合は、Ｃ君、Ｄ君の２人が選ばれる１通りです。このときも、「Ｃ君とＡ君」「Ｃ君とＢ君」の選び方を数えてはいけません。これらをすべて合わせたらよいので、学級委員の選び方は、３＋２＋１＝６(通り)です。

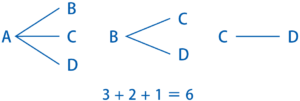
・解き方のポイント
２人の学級委員に区別はないので、「Ａ君とＢ君」が選ばれる場合と「Ｂ君とＡ君」が選ばれる場合は同じです。Ａ君が選ばれる場合、Ｂ君が選ばれる場合と順番に樹形図を画き、重複して数えないように注意しましょう。

・別の解き方
組み合わせの問題であることがわかれば、組み合わせの公式を使って解くことができます。４人の中から２人を選ぶので、（４×３）÷（２×１）＝６（通り）となります。

●例題３【サイコロ】

・問題
大小２個のサイコロを同時にふります。出た目の合計が５の倍数になる場合は何通りあるか求めなさい。

・答えと解き方
答え：７通り

出た目の合計が５の倍数となるのは、合計が５または10のときです。そこで、どのような目が出たときに合計が５または10になるか、それぞれについて調べます。

合計が５になるのは、（大，小）＝（１，４）、（２，３）、（３，２）、（４，１）の４通り
合計が10になるのは、（大，小）＝（４，６）、（５，５）、（６，４）の３通り

したがって、出た目の合計が５の倍数となるのは、４＋３＝７通りです。

・解き方のポイント
ある事柄ＡとＢについて、ＡとＢが同時に起こらないとき、ＡまたはＢが起こる場合の数は、Ａが起こる場合の数とＢが起こる場合の数を足し合わせたものになります。これを「和の法則」と呼びます。

当たり前のことですが、大小のサイコロの目の合計は、同時に５と10にはなりません。そのため、この問題では和の法則を利用して、答えを求めることができます。

●例題４【道順】

・問題
３つの地点Ｘ、Ｙ、Ｚがあります。ＸからＹへの行き方は３通りあり、ＹからＺへの行き方は４通りあります。ＸからＹを通ってＺへ行く道順は何通りあるか求めなさい。

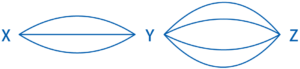
・答えと解き方
答え：12通り

ＸからＹまでの３通りの行き方をそれぞれ①、②、③とすると、①の行き方を使ってＹまで行き、そこからＺまで行く道順は４通りあります。同じように、②、③を使ってＹまで行く場合も４通りずつあるので、ＸからＹを通ってＺまで行く道順は、４×３＝12（通り）です。

・解き方のポイント
ある事柄ＡとＢについて、ＡとＢが同時に（または続けて）起こるとき、ＡとＢが起こる場合の数は、Ａが起こる場合の数とＢが起こる場合の数を掛けたものになります。これを「積の法則」と呼びます。

この問題では、まずＸからＹへ行くという事柄のあと、続けてＹからＺへ行くという事柄が起きるので、ＸからＹを通ってＺへ行く道順は、積の法則を使って求めることができます。

---

中学受験頻出の「場合の数」は、さまざまなパターンの問題に慣れておこう

「場合の数」は中学受験に頻出の単元です。苦手意識を持っている受験生も多いでしょうが、しっかりマスターすれば得点源にできます。「場合の数」の問題を解くポイントは、数え間違いをしないこと、どの数え方をすればよいかを見極められるようになることです。そのためには、多くの問題にあたって、演習を繰り返すことが大切です。

「京進の中学・高校受験 TOPΣ」では、「場合の数」のさまざまなパターンの問題に取り組めます。問題を十分に考えたあとに丁寧な解説を受けることによって、解き方を自分のものにできるはずです。興味のある方は、お近くの校舎までお気軽にお問合せください。

お近くの「京進の中学・高校受験TOPΣ」校舎を探す