
- 中学受験
中学受験で出題される「速さ」の苦手を克服!頻出問題と解き方のコツ
算数における「速さ」は得意不得意が分かれる単元です。平均の速さを求める簡単な問題から、つるかめ算の考え方を利用する問題などのような入試問題に出てくる受験算数まで、幅広い難易度の問題があります。
「速さ」の問題が苦手だという悩みがある小学生は、公式が頭に入っていなかったり単位変換を理解していないことが多く、その2点を完璧にすることができれば正解率は上がるでしょう。
この記事では、中学入試で出題される「速さ」の問題が苦手という小学生に向けて、頻出問題と解き方のコツを紹介します。攻略法があるわけではありませんが、この記事を読んで「速さ」問題の理解を深めてください。
本記事の目次

中学受験で必須!速さの基礎知識
中学受験で必ずと言ってよいほど出題される速さの問題。まずは、速さの基礎から確認していきましょう。速さは、受験対策としてだけでなく、大人になってから日常生活の中で使う知識としても重要です。絶対に頭に入れておいてほしいポイントをまとめているので、参考にしてください。
速さの意味や単位、公式をまず理解して覚えましょう。算数は社会や理科よりも暗記することが少ない科目ですが、公式だけは覚える必要があります。
完璧に覚えられるまでは単位や公式をまとめて書き、よく見る場所に貼っておくのもおすすめです。テストの時、思い出すのに時間がかからないように、悩まずにスラスラ言えるまで練習しましょう。
速さを学ぶ上で、時間の単位も理解しておく必要があります。算数では時刻が出てくる問題は非常に多いので、時間の単位や概念の復習もしておくとよいでしょう。
速さの意味や単位
速さは一定の時間あたりに進む道のりのことです。速さの単位として時速、分速、秒速の意味を理解しましょう。時速は1時間あたりに進む道のり、 分速は1分間あたりに進む道のり、 秒速は1秒間あたりに進む道のりを表します。
1kmは1,000mであることも忘れないようにしましょう。kmとmのどちらで答える問題なのか注意するとよいでしょう。
・時速=1時間で進む道のり(単位:時速〇km、〇km/時)
・分速=1分間で進む道のり(単位:分速〇m、〇m/分)
・秒速=1秒間で進む道のり(単位:秒速〇○m、〇m/秒)
速さの3公式
速さの問題は3つの公式を上手く使うことで答えを導けます。
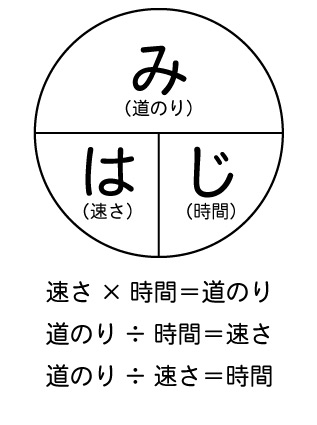
公式を全部覚えるのが難しく感じる場合は、以下の図を1つ覚えておくことで3公式を簡単に作り出すことができます。ミスを減らすためにも、線分図や面積図を使って情報を整理してから公式を使うのがおすすめです。
*速さの3公式
・速さ=道のり÷時間
・道のり(距離)=速さ×時間
・時間=道のり÷速さ
速さの問題が苦手な原因と克服するためのポイント
苦手を克服するには、間違った原因や自分の置かれている状況の分析が必要です。以下では、速さの問題が苦手な小学生に見られる間違った原因を3つ紹介します。苦手の克服に役立ててください。
原因1:機械的に計算している
速さの基本である「一定の時間あたりに進む道のり」の意味を理解できているでしょうか。この意味が理解できないと、機械的に公式へ数字を当てはめて計算することになり、応用問題に対応するのが難しくなります。
次に紹介する単位変換にも関わる内容ですが、速さの問題は公式を暗記するだけでは攻略できません。
問題をよく読み、公式に当てはめるだけで解けるのかどうかを即座に見分けられるようになりましょう。速さの問題は「一定の時間あたりに進む道のり」を導き出すことが重要です。簡単な問題を解きながら、速さの本質を捉えることから始めましょう。
原因2:単位変換の重要性を理解していない
速さの問題を解く上で、単位変換を正確に行うことは要となります。複数の単位を意図的に組み合わせて、複雑にしている問題でつまずいているケースは、この単位変換ミスが目立ちます。
例えば、時速40kmのバイクが30分で進む道のりを求める問題。時速40kmで30分進む道のりは、30分では計算できないということに気づき、30分=0.5時間になおしてから計算しなければいけません。分数や小数を使って単位を揃えることを習慣化し、単位の変換、式の計算の順で解くことが大切です。
原因3:割合や比と速さがリンクしていない
速さの問題に苦手意識を持つ3つ目の原因として、割合や比と速さがリンクしていないことが挙げられます。
速さの問題を解くには、割合や比の考え方を使う必要があります。「速さ」とは、時間あたりの変化の「割合」を考えるものでもあるからです。割合や比と速さを関連させて考えられるようになると、応用問題に対応しやすくなります。単位変換や公式を頭に入れた上で割合や比、逆比の考え方も得意にしていけるとよいでしょう。
\生徒ひとりひとりに合った指導で志望校合格へ導く/
中学受験でよく出る速さの例題と解き方
頻出問題は入試において得点を確実に取るチャンスです。短期間で受験の対策がしたい場合は、特に頻出問題に力を入れるとよいでしょう。以下では中学受験でよく出る、速さの例題3題とその解法を説明します。
例題1
兄と弟が3km離れた地点から向かい合って同時に出発しました。兄は分速45m、弟は分速30mで歩いています。2人が出会うのは出発してから何分後ですか?

例題2
速さが一定である電車が500mの鉄橋を渡り始めてから渡り終わるまでに30秒かかり、800mの鉄橋を渡り始めてから渡り終わるまでに45秒かかります。この電車の速さは秒速何mですか。

例題3
流れの速さが一定である川の36km離れた2地点間を、静水時の速さが一定である船で往復すると、上りは3時間、下りは2時間かかります。この船の静水時の速さは時速何kmですか。

基本問題よりレベルアップした応用問題では、グラフを利用する力も必要です。上の問題が解けた人は、ダイアグラムから読み取る問題や時計算、比を使った問題にもチャレンジしてみてください。
速さの問題を得意にして中学受験を乗り切ろう
速さの頻出問題と解き方のコツを紹介してきました。速さの問題は、まず公式の暗記と単位変換が必要です。間違えた問題は途中式や線分図を確認し、対策をすることも大切です。
中学受験対策は、有名中学から最難関中学まで挑戦できる確かな実力をつけられる京進の中学・高校受験TOPΣ「中学受験コース」におまかせください。最後の授業が19時までという通いやすい時間なので、生活リズムを崩すことなく受験生の勉強をサポートできます。学校の宿題や家庭学習の時間も確保できるでしょう。
無料体験も開催しているので、ぜひお近くの校舎へお問合せください。











